티스토리 뷰
"해당 포스팅은 Dan Jurafsky 와 Chris Manning 교수의 2012년 Stanford NLP 강좌를 정리한 내용입니다."
석사논문 쓰면서 수없이 봤는데 누가 설명해보라고하면 자신 없을 것 같았던 N-gram language model 드디어 정리해본다. 우선 Probabilistc language model 이란 뭐냐? Sentence / phrase 가 주어졌을 때 그게 얼마나 likely 한지를 probability 로 나타내는 모델임.
그럼 그걸 어떻게 계산하냐? 2가지 방법이 있다. 첫번째로 Joint probabilty 인 P(W) 즉, P(w1,w2,w3...wn−1,wn) 을 구하거나 아니면 conditional probabilty of a last word given previous words 즉, P(wn|w1,w2,w3...wn−1) 로 구할 수 있다.

그럼 joint probability model 부터 살펴보자. Joint probability P(its,water,is,so,transparent,that) 을 구해보자. 이 때, 우리에게 필요한 건 Chain Rule of Probability
그럼 Chain Rule 이 뭐냐? 옛날 옛적 확률과 통계 배우던 시절의 기억을 되살려 보자.
P(A|B)=P(A,B)P(B)
P(A,B)=P(A|B)P(B)
위 식을 통해서 joint probability가 conditional probability of A given B * probability of B 로 나타낼 수 있다는 있게 됐다. 이 식만 있으면 A,B 의 joint probability 뿐만이 아니라 더 많은 variable 의 joint probability, 예를 들어 P(A,B,C,D) 같은 것도 나타낼 수 있다.
결국 chain rule 을 통해서, n 개의 variable 에 대한 joint probability 를 다음과 같이 조건부 확률을 표현해서 나타낼 수 있다.
P(x1,x2,x3,...,xn)=P(x1)P(x2|x1)P(x3|x2,x1)...P(xn|x1,...,xn−1)

좀 더 formal 하게 표현해보자면, sequence of words 의 joint probability 는 다음과 같이, previous words 에 대한 last word 의 조건부 확률의 product 로 나타낼 수 있다. 단어로 치환해서 생각해보면 첫번째 단어가 올 확률, 1번째 단어가 주어졌을 때 2번째 단어가 올 확률, 1-2 번째 단어가 주어졌을 때 3번째 단어가 올 확률... 이런 식으로 계속 나아간다.

그럼 식을 이렇게 나타내긴 했으니까 maximum likelihood 를 통해서 엄청 큰 corpus 를 가지고 2개의 문장 "its water is so transparent that" 과 "its water is so transparent that the" 의 occurence 를 다 센 다음에 나누면 되는거 아니야? 라고 간단하게 생각할 수도 있지만.. 실제로는 문장이 길수록 해당 문장이 rare 할 것이기 때문에 그걸 다 세서 probability 를 estimate 할만한 충분한 양의 데이터를 모으는게 거의 불가능하다.

그럼 어떻게 구할 수 있을까? 정확하진 않지만 식을 단순화 하기 위해 필요한 어떤 가정 => Markov assumption 을 통해서 가능하다. 아래에서 보는 것처럼 whole previous sequence 가 주어졌을 때 last word 로 'the' 가 나올 확률을 마지막 2 개의 단어 (transparent that) 이 주어졌을 때 'the' 가 나올 확률이랑 비슷하다고 assume 하는게 바로 그 가정이다.

바로 이전에 chain rule 을 통해서
P(w1,w2...wn)=∏P(wn|w1,w2...wn−1) 로 나타낼 수 있었던 것이 Markov assumption 을 통해서 다시 P(w1,w2...wn)=∏P(wn|wn−k,w2...wn−1) 로 표현이 가능해진 것!
다시 말하자면 previous sequence 에 대해서 last word 의 probability 를 last few words 에 대한 last word 의 probability 로 유사하다고 가정을 하는 거임. 이 때, last few words 가 몇 개냐에 따라서 bi-gram, tri-gram model 이 되기 때문에 n-gram 모델이라고 부른다.

당연히 가장 심플한 모델은 n=1 일 때, 즉 uni-gram 모델이다. 어떤 sequence 의 probability 를 단순히 각 단어의 probability 의 product (곱) 으로 나타내는 모델이다.

n=2 일 때는 bi-gram 모델. entire previous words 에 대한 last word 의 확률을 previous word 1개에 대한 last word의 probability 로 구하는 것!

물론 단순화하는 가정때문에 long-distance 를 catch 하는 데에는 부족한 모델이긴 하지만, 실제로는 웬만한 건 어느정도 할 수 있어서 오랫동안 광범위하게 사용됐던 모델이다.

이제 markov assumption 을 통해서 식을 간단하게 만드는데 성공했으니 n-gram 모델을 사용해서 직접 probability 를 estimate 하는 것이 남았다. 아까는 sequence 가 길어질 수록 occurrence 가 너무 rare 하기 때문에 count 하기 위해서 충분한 데이터를 모으는게 거의 불가능했다. 하지만 이제는 n-gram occurence 를 count 하면 되기 때문에 maximum likelihood estimate 을 통해서 다음과 같이 P(wi|wn−1) 을 각각 wi−1, wi 의 co-occurence 그리고 wi−1 의 occurence 를 세서 계산하는 것이 가능해졌다. 모든 vocabulary 의 occurence 와 모든 vocabulary 의 단어의 bi-gram 조합에 대해서 co-occurence 를 세고 이것을 바탕으로 probability 를 계산한 것이 모델의 parameters 라고 할 수 있음.

이런 식으로 bigram count 를 모두 기록하는 table 이 필요하겠지. 표에서도 보이다시피 bi-gram 도 대부분의 경우 0 의 값을 갖는 걸 볼 수 있다.
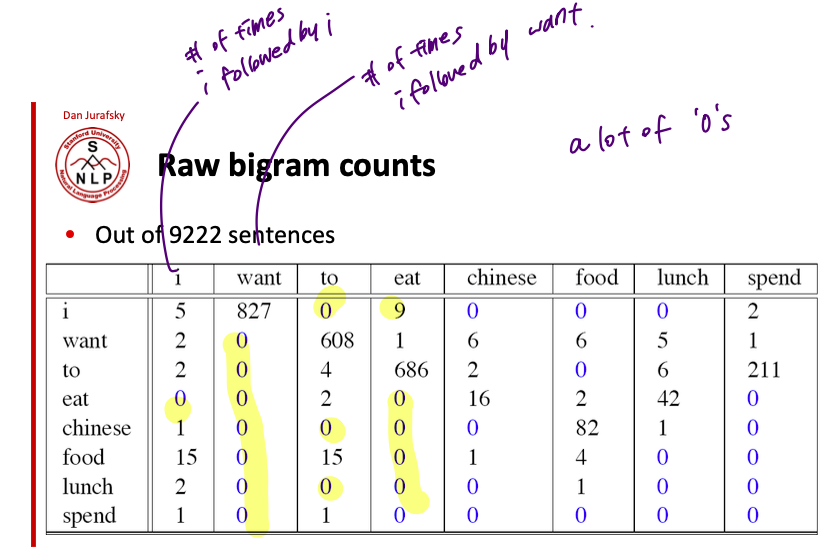
그리고 bigram 카운트를 셌으면 이걸 가지고 다시 unigram count 로 나눠야지. 아래의 table 처럼 각 bi-gram 의 probability 가 bi-gram model 의 parameters 이다.
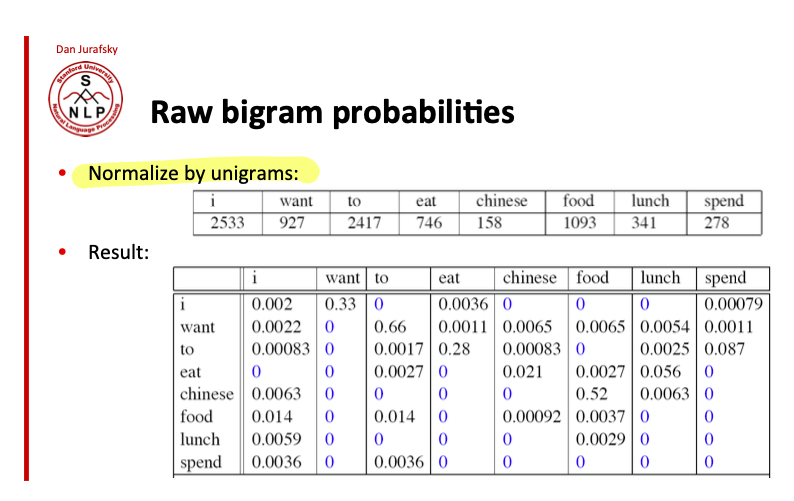
그럼 이 테이블을 가지고 어떤 sequence 가 주어졌을 때, 해당 sequence 의 probability 를 반환할 수가 있게 되는거임. 아래의 예시처럼 "I want english food" 라는 문장의 proability 를 구하고 싶다면, 각 bi-gram 의 probability 를 곱하면 되는 거임.

그런데 결과값으로 매우 작은 값 0.000031 이 나오는 것을 알 수 있다. 문장에 포함된 bi-gram 의 probability 가 낮을 수록 그 값을 모두 곱하면 너무 x 100 작은 값이 나오기 때문에 실제로는 log probability 를 통해서 값을 계산한다. underflow 를 피하는데도 좋은 방법이지만 실제로 컴퓨팅 측면에서도 multiplying 보다 더하는게 빠르기 때문에 log probability 를 사용한다. log 의 특성상 아래 식처럼 값의 곱을 log 의 합으로 나타내는 게 가능하기때문에.

'NLP > 이것저것' 카테고리의 다른 글
| Dependency parsing (0) | 2022.06.08 |
|---|---|
| Transformer / BERT / GPT2 / BART 의 차이 (0) | 2021.12.30 |
| Naïve Bayes Classifier (0) | 2021.12.06 |
| Accumulated gradients (0) | 2021.08.03 |
| Word embedding vs Contextual embedding (0) | 2021.05.04 |
- Total
- Today
- Yesterday
- 워터마킹
- 언어모델
- 벡터
- Neural Language Model
- Attention Mechanism
- 뉴런
- language model
- GPTZero
- Bert
- cs224n
- Statistical Language Model
- Elmo
- 뉴럴넷
- LM
- Contextual Embedding
- word embedding
- neurone
- weight vector
- transformer
- Pre-trained LM
- nlp
- neural network
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
