뉴럴 네트워크 & 뉴런 - units 개수와 weight shape 이해하기!

오마이갓... 드디어 시원하게 벡터와, 뉴럴넷 이미지를 연관시켜서 이해함. 그동안 그렇게 봐도 이해가 안 됐던 데는 이유가 있었음. 다시 한번 뉴럴넷 (input layer - hidden layer - output layer 로 이루어진) 과 벡터를 함께 보면서 이해를 해보자.  

 

우선, 딥러닝에서는 모든 것이 colum vector 기준. 

예를 들어서 우리가 데이터 하나를 가지고 있는데, Features 가 3개가 있다. 이걸 벡터 혹은 행렬로 나타내라고 한다면  $\begin{bmatrix}
 x_{1} \quad x_{2} \quad x_{3}
\end{bmatrix}$  가 자연스럽게 느껴짐 (나만 그런가..?). 그렇지만 벡터에서는 colum vector 기준이기 때문에  $\begin{bmatrix}
 x_{1}
\\ x_{2}
\\x_{3}
\end{bmatrix}$ 로 표현된다.

 

뉴럴넷을 간단하게 표현해봄. 실제로는 각 unit 을 통과할 때 마다 activiation function 도 있음.

 

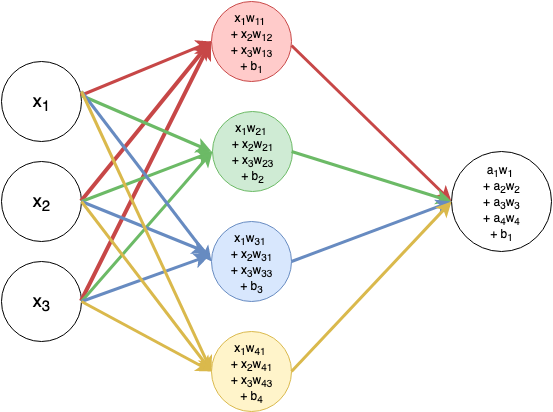
[3개의 Features 를 가진 데이터 1개] 를 [4개의 units 를 가진 hidden layer] 에 통과시켜서 [최종값 y를 내는 하나의 unit 을 가진 output layer] 가진 뉴럴넷을 표현한 그림이다. 이 그림을 각각의 unit 에 혹은 layer 에 해당하는 벡터와 함께 나타내 보자. 

 

최대한 간단하게 표현하기 위해서 각각의 layer 의 weight 을 구분하지 않음. 원래는 $w^{[1]}_{(11)}$ 처럼 각각의 layer 와 unit 를 구분하는 transcript 필요.

 

여기서도 보이듯이 각 벡터는 column vector 라서 각각의 column 이 하나의 set 임. 근데 좀 이상한 게 있다. input vector 가 (3 x 1) 벡터고, hidden layer 의 벡터가 (3 x 4) 벡터면 $ x * w $ 서로 곱을 할 수가 없음. 그래서 hidden layer 의 weight vector 를 전치행렬로 바꾼 다음에, x 행렬 앞에 갖다 붙이면 $w^{T}x$ 이고  (4 x 3) x (3 x 1) 벡터가 되기 때문에 출력값으로 (4 x 1) 의 벡터를 갖게 된다. - 계속 그림이랑 연결시켜서 생각하면 좀 더 쉽게 이해 됨. 

 

그러면 이 hidden layer 의 output - a -  은 다음 layer (output layer) 의 input 이 되는 거고,  ouput layer 가 가진 weight output 역시, 전치행렬을 취한 다음,  a 앞에 곱해주는 거임 - $w^{T}a$ 그러면 출력값으로 label 에 해당하는 1개의 scalar value 를 값으로 갖게 된다! 

 

근데 이것을 수식으로 표현할 때는  $w^{T}x$ 에서 종종 전치행렬에 해당하는 T 를 빼버리고 $Wx$ 로 나타낸다. 그리고 그렇기 때문에 weight vector 는 좀 더 익숙하고 직관적인 row vector 처럼 표현되는 거임. \begin{bmatrix}
w_{11} &w_{12}  & w_{13}  \\ 
w_{21} &w_{22}  & w_{21} \\ 
w_{31} &w_{32}  & w_{33}\\ 
w_{41} &w_{42}  & w_{43}  
\end{bmatrix}

 

결론적으로 내가 저 그림과 벡터만 보면 헷갈렸던 이유는 첫째, 벡터를 쓸 때는 보통 column vector 라고 하는 걸 몰랐기 때문에. 둘째, weight vector 가 tranpose 돼도 종종 T 를 생략한다는 것을 몰랐기 때문. 그래서 저 그림을 볼 때마다, 뭐야 어떤 벡터는 row vector 고 어떤 거는 column vector 고 엉망진창이야!! 하고 이해를 포기했던 sad story .. 

 

앞으로는 그냥 간단하게 weight vector 를 제외한 모든 벡터는 column vector 고, weight vector는 row vector 라고 생각해버리자! 

 

그리고 각 layer가 가지고 있는 (이미 trasnpose 된) weight vector의 크기, 혹은 shape 은 [units 개수 x input 개수] 인데 units 개수 = outputs 개수임 (3개의 features 4 개의 units 에 통과시키니까 4개의 outputs 이 나오므로). 왜 input 개수가 뒤에 오는지는 알겠지? 뒤에 input vector 를 곱하기 때문. 

 

previous hidden layer 의 output 이, current layer 의 input 이 되므로, 각 layer 의 weight vector shape 은 다음과 같다. 계속 $W*a$ (a는 이전 layer 의 output 이자, 현재 layer 의 input) 인 걸 생각하면 쉬움. 

 

 

각 layer 의 weight shape